\( \DeclareMathOperator{\abs}{abs} \newcommand{\ensuremath}[1]{\mbox{$#1$}} \)

The premise of this exercise is, that a sample-rate
of 96kHz is assumed, and that all 67 frequencies
from 300Hz to 20.1kHz will be phase-delayed by 90 degrees.

Therefore, a Discrete Sine Transform is to result
in the suitable convolution.

(%i1) conv: [];
\[\tag{conv}\label{conv}[]\]
(%i2) for i: 1 thru 320 do
   conv: cons(0, conv);
\[\tag{\%{}o2}\label{o2} \mathit{done}\]
(%i3) for k: 0 thru 159 do
   for n: 0 thru 67 do block (
       conv[160 + k]: conv[160 + k] + (sin((n*k*%pi)/160) / 160),
       conv[160 - k]: conv[160 - k] - (sin((n*k*%pi)/160) / 160)
   );
\[\tag{\%{}o3}\label{o3} \mathit{done}\]
(%i4) load(draw)$
\[\mbox{}\\\mbox{;; Loading "/home/dirk/.maxima/binary/5\_ 38\_ 1/gcl/GCL\_ 2\_ 6\_ 12/share/draw/grcommon.o"}\mbox{}\\\mbox{;; Finished loading "/home/dirk/.maxima/binary/5\_ 38\_ 1/gcl/GCL\_ 2\_ 6\_ 12/share/draw/grcommon.o"}\mbox{}\\\mbox{;; Loading "/home/dirk/.maxima/binary/5\_ 38\_ 1/gcl/GCL\_ 2\_ 6\_ 12/share/draw/gnuplot.o"}\mbox{}\\\mbox{;; Finished loading "/home/dirk/.maxima/binary/5\_ 38\_ 1/gcl/GCL\_ 2\_ 6\_ 12/share/draw/gnuplot.o"}\mbox{}\\\mbox{;; Loading "/home/dirk/.maxima/binary/5\_ 38\_ 1/gcl/GCL\_ 2\_ 6\_ 12/share/draw/vtk.o"}\mbox{}\\\mbox{;; Finished loading "/home/dirk/.maxima/binary/5\_ 38\_ 1/gcl/GCL\_ 2\_ 6\_ 12/share/draw/vtk.o"}\mbox{}\\\mbox{;; Loading "/home/dirk/.maxima/binary/5\_ 38\_ 1/gcl/GCL\_ 2\_ 6\_ 12/share/draw/picture.o"}\mbox{}\\\mbox{;; Finished loading "/home/dirk/.maxima/binary/5\_ 38\_ 1/gcl/GCL\_ 2\_ 6\_ 12/share/draw/picture.o"}\]
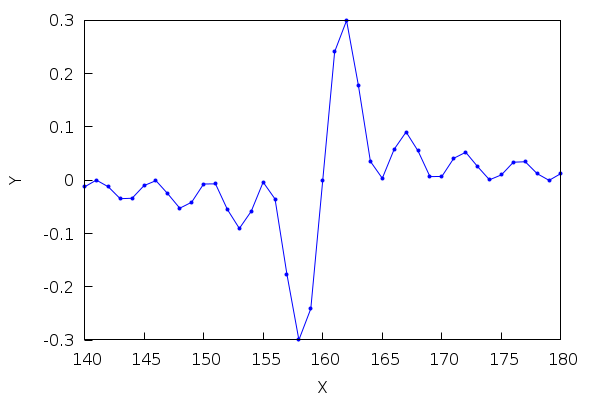
(%i5) ToPoints() :=
   makelist([i, conv[i]], i, 140, 180);
\[\tag{\%{}o5}\label{o5} \operatorname{ToPoints}():=\operatorname{makelist}\left( [i,{{\mathit{conv}}_{i}}],i,140,180\right) \]
(%i6) wxdraw2d(
   point_type = filled_circle,
   point_size = 0.5,
   points_joined = true,
   points(ToPoints()) )$
\[\tag{\%{}t6}\label{t6} \] (Graphics)
(%i7) float([conv[156], conv[157], conv[158], conv[159], conv[160], conv[161],
       conv[162], conv[163], conv[164]]);
\[\tag{\%{}o7}\label{o7} [-0.03531432161002312,-0.1773375347935022,-0.2995056375354308,-0.2409554237325049,0.0,0.2409554237325049,0.2995056375354308,0.1773375347935022,0.03531432161002312]\]
(%i8) F(x) := (1 - cos(x*%pi)) / (x*%pi + (signum(x) * 0.002) + 0.001);
\[\tag{\%{}o8}\label{o8} \operatorname{F}(x):=\frac{1-\cos{\left( x\ensuremath{\pi} \right) }}{x\ensuremath{\pi} +\operatorname{signum}(x)0.002+0.001}\]
(%i9) G(x) := sin(x) / x;
\[\tag{\%{}o9}\label{o9} \operatorname{G}(x):=\frac{\sin{(x)}}{x}\]
(%i10) G_a(x) := G((abs(x) * %pi) + 0.001);
\[\tag{\%{}o10}\label{o10} {{G}_{a}}(x):=\operatorname{G}\left( \left| x\right| \ensuremath{\pi} +0.001\right) \]
(%i11) wxplot2d([F(x), G_a(x)], [x,-8,8])$
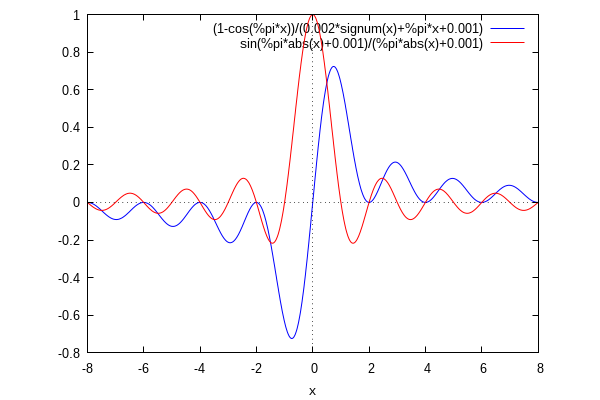
\[\tag{\%{}t11}\label{t11} \] (Graphics)

An interestting fact to point out would be, that
an amplitude-uniform 90-degree phase-shift will
always be possible, only down to some lowest
frequency. The continuous function above, only
guarantees that this will work down to 3kHz.

(%i12) float([F(0.5) - F(1.5), F(2.5) - F(3.5)]);
\[\tag{\%{}o12}\label{o12} [0.4233346540208565,0.0363544636913025]\]
(%i13) float([F(1) - F(3), F(5) - F(7)]);
\[\tag{\%{}o13}\label{o13} [0.4238733604118996,0.03636636524925749]\]
Created with wxMaxima.