This 3D model was first created randomly using a program called "Creature Creator 1.7 Pro." In today's world, the term "model" can refer as easily to a kind which only exists as data, as it can to a kind which is made of plastic or other materials. And either way, some workers need to spend a lot of time defining or sculpting models, for example so that they can be used for CGI instead of being filmed the old-fashioned way. I call this one 'Kthalaha.' Next I used a program called "Poser 6" to give her an internal skeleton, which is called "rigging," and which also allows me to apply any out of a library of predefined poses to the model, such as the fighting stance shown. I suppose that in fighting such a creature, an added concern would be that it could grab us, and then fly off with us. Or drop us from 200 feet in the air. But humans don't need to worry about that since winged humanoids don't really exist. And of course you're not actually looking at the 3D model itself, for which you'd need to open a different type of file with a program that most of you may not have installed. You're just looking at a rendered, 2D perspective of my 3D model.

In order for the internal skeleton, which remains invisible, to have any effect, groups of polygons on the model's surface need to be attached to each bone. These polygons must also exist if the model corresponds to a dancing skeleton, because on the computer what we see isn't the actual data-skeleton, just a narrow mesh that looks like bones then. And this grouping step could take more time to carry out with care. But with Poser 6, I used an automatic grouping tool alone, for which reason certain surfaces appear disconnected from the body. Poser 6 automatically grouped parts of the wings with animation anchors such as ?hands? because in the mind of this one program, there is no allowance for non-human wings.

And for more serious use, I should also give her a realistic surface texture, instead of continuing to pretend that her species evolved something other than skin. And I could also grow simulated hair on additionally-selected groups of polygons...

There are two, more practically-oriented notes I wanted to mention, about animating models using bones. Firstly, the animation below shows a crack along the creature's abdomen, because the vertices were not blend-skinned. And secondly, skeletal animations are transferable.

I've found out that the model-sections in question were not blend-skinned, because the stored animation file (I'll get to .BVH Files in a moment) was missing an extra bone's definition for one of the bones the Poser 6 humans generally tend to have in their spine. While this shouldn't cause any problems, in practice each vertex along this crack fails to get linked to an adjacent bone, because that adjacent bone is missing, and because the software fails 'to skip to the next bone after that', when we apply the .BVH File.

"Blend-skinning" is a technique supported by modern GPU-bones / Vertex Shaders (for real-time use in games), in which the structure of each element of the vertex array has not one bones number, but two bones numbers plus a blend-weight for each of these bones. In fact, blend-skinning exists today, by which a vertex is attached to up to 4 bones. Vertices around joints should in fact be modelled as attached to at least 2 bones, with variable weights, so that as these bones move, belonging to the current joint, vertices will make the transition gradually, from moving with the parent bone, to moving with the child bone. Otherwise, we will obtain a crease along a joint - such as along an abdomen - where vertices are suddenly modelled to move with the new child-bone.

It can be understood, that each bone can have an associated bones matrix, the inner 3x3 sub-matrix of which specifies one rotation, and the 4th column of which specifies a displacement - thus also defining where the (non-zero) hinge-point is, around which the bone rotates. Then, the game- or rendering-engine can fill the rotation matrix with trig functions of the (3D) Euler angle of the rotation, and the result can be displaced as needed, for example such that the hinge point does not move... What some people may infer from this, is that in order to make use of skeletal animations, the game- or rendering-engine must always feed in the Euler angles etc..

Thankfully, there is "a more pragmatic way to organize skeletal animations", which has the same simplcity numbered frames had for vertex animations. In the case of vertex animations, there used to be a default frame that defined the basic shape of the model, through the use of a vertex array and a triangle list, followed by animation frames, which essentially offered a new vertex array each, to redefine the shape of the whole model. This simplcity is much desired by game authors, although much memory is wasted by restating, effectively, the whole set of 3 coordinates for every vetex, for every choreographed frame.

Well pratical model files may not only possess 'vertex frames', but also 'bones frames'. What bones-animation frames do when stored in a model file, is only to restate the bones matrix for each defined bone, while keeping the default vertex geometry. Usually, a full set of bones matrices will consume less storage, than a full repetition of the vertex geometry. And yet these model files will allow a game to select a bones frame, just as easily as to select a vertex frame... Thus when writing game scripts, it can sometimes be much easier just to do so, than it was to have to (compute-and-)set the 3D Euler angles for every joint. The only real exception comes up when there is supposed to be 'Games Physics'.

In fact, such pragmatism goes further. It's rarely required for a bone to change in length, only to rotate and have a hinge-point. Well the bones that make up rigged models have names, and a file-format exists, to export and import lists of bones-names, along with a changing matrix for each bones-name. This file format I'm referring to is the 'Biovision .BVH File'. Then, if the actual skeleton we apply a .BVH File to is missing any bone by a given name (as stated in the .BVH File), all we get is a trivial warning message. If the .BVH File is missing specifications for bones defined in the model file, those bones don't move. But after we've applied this kind of a .BVH motion-capture file to a new model, we end up with updated bones-matrices for the new model [:*], and with the bones-frames as well, that can be stored in the model-file in question and evoked by a simple script.

This example below uses the rigging from above, and applies such a (purchased) .BVH File's boxing moves, without ever having required me to compute the Euler angles of any joint... Important: If we purchase any .BVH Files, we need to make sure that the seller has not committed any copyright infringements, as the buyer would also be doing so, if he then incorporated those (stolen) Animation Sequences into a game, which we'd next maybe like to sell. Thus, one should also ask oneself whether a seller of .BVH Files did have the resources actually to do motion capture, and actually to ask such a seller to show us footage of his motion capture sessions, which he should have in abundance...

*] Actually, Poser gives me a hint as to what this motion-capture file really contains, by asking me when I apply it, whether I'd like it "to scale" the animations to the current model. By selecting this option, I'm forcing Poser to recompute the displacement vector within each matrix, such that the hinge-point, which only Poser stores, does not move. Therefore, the .BVH File does not contain actual Euler angles, which would be independent of the model's scale, but matrices, the 4th (displacement-bearing) column of which may be inconsistent with the lengths of all the bones, of the model I'm applying it to. We would only choose not to scale motion-capture files, if they are supposed to do more than rotate bones around their hinge-point, at which time we're also asking for trouble... And, while the imported, inner 3x3 matrices are capable of scaling the vertices as well, I'm assuming that Poser detects this and neutralizes it, when we select this opion.

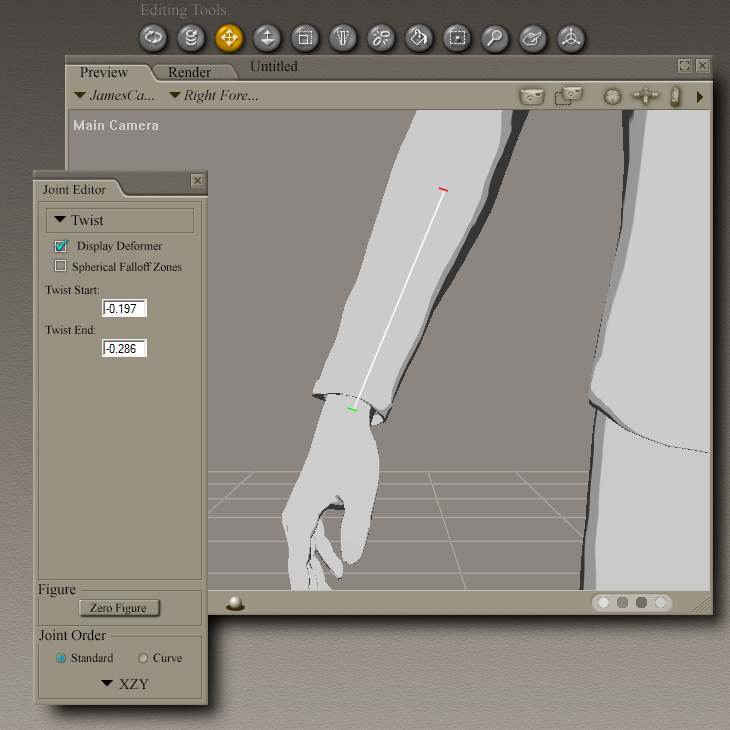
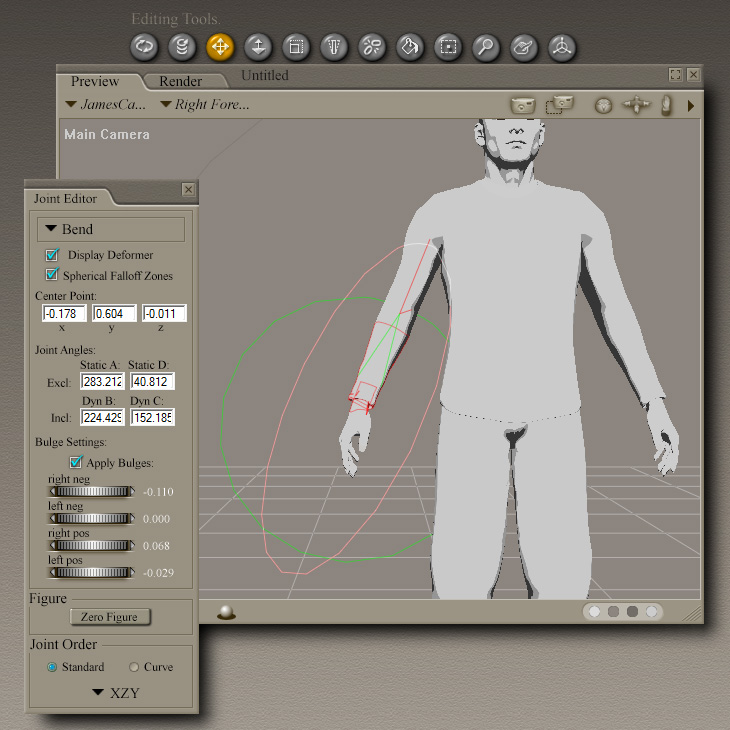
One reason fw I did not take the time to blend-skin this model, was laziness. Another reason is the fact that Poser has its own, HQ techniques, to fine-tune each joint. These techniques allow for spherical fall-off regions around each joint if wanted, but also break down the bones' movements into the Euler angles 'Roll', 'Tilt' and 'Pan', which Poser names "Twist", "Bend" and "Side-Side", such that we can specify a separate fall-off zone for Twist let's say, from the fall-off zone Bend would have. This allows a forearm to twist properly for example. But it's virtually certain that these Poser techniques of blending the effect of bones and joints, will not export properly into the world of game engines, where each vertex only has one blend-weight, for each bone it's attached to.

Hence, if I'm aiming to use Poser just as a model editor, for animating models within another program, I cannot really rely on these features. In fact, (my, purchased) Poser 6 still had the drawback, that when exporting model files, it would fail to export the skeletons and rigging along with them. And this was really due to the limited slection of file formats exported to. Therefore, it makes more sense to use Poser as the rendering platform as well, not just as a model editor... Yet, I have other model editors, more suited to game-design. Also, I don't know whether this limitation still exists with 'Poser 2014', so that of course the reader would make his own assessment of any product, before buying it for themselves.

**] I just wanted to add a hint, for how it's possible to start with a 3x3 rotation matrix, and to find the inverse-trig Euler angles from it. In case the 3x3 is not a pure rotation, I suppose it would be possible to do an orthonormalization of it first, but I'm not sure it's strictly necessary in this context. What I do expect, is that each column of it has been made a unit vector...

The trick to visualizing a bone-angle as a Euler, is in the assumption that in its relaxed position, the bone is facing 'straight up', i.e. with an angle of elevation of 90 degrees, defining the Z-component of its own vector space. It's helpful when model editors are given, roughly which coordinate in model space this corresponds to. The current bone's 'Tilt' is the negative angle with which it bends 'down' from this position, thus also forming its degree of 'Bend'. And the 'Pan' now becomes the angle which it forms after it has bent, assuming a consistent set of X and Y -component vectors at the base of the bone. Therefore, the first task one would need to perform, is to establish this set of X-, Y- and Z-component-vectors, that are unique to one bone.

To do that, one does not only need the 3x3 matrix, but also a segment representing the bone in its unbent, neutral orientation. Its vector is also the mentioned Z-component. I think that the best strategy involves multiplying this Z-vector by the matrix and thus rotating the bone into the defined position. But in order to get any further with this, the X- and Y-vectors need to be defined.

In order for the bone-X and bone-Y vectors to form a meaningful plane at the base of the bone, the known bone-Z can be crossed with any real-world vector, say model-Z, forming the bone-Y-vector. This bone-Y can then be re-crossed with bone-Z, to find the bone-X, which will be perpendicular with bone-Z, yet best-aligned with model-Z. Model-X, or model-Y can be switched in, as bone-X.

Once the bone has been given its own coordinate system, which did not require any application of the matrix yet, the rotated bone can be positioned within this system, so that the angles can also be found. For that, one operation which might be useful, is to subtract the orthogonal projection of any rotated bone, along bone-Z, so that only the corresponding vector in the plane of bone-X and bone-Y remains. Its absolute would be the sine of the angle of Bend, while the dot-product of the rotated bone with bone-Z gives the cosine of the angle of Bend (which would already be enough). But if the planar component of the rotated bone angle within bone-X and bone-Y is normalized, then its bone-X forms the cosine, and its bone-Y the sine of the Euler angle of Pan, aka the angle of 'Side-Side'.

Finding the angle of 'Twist' is a bit more tricky, in that I think a second vector needs to be matrix-multiplied, and the best vector to start with might be the cross-product of the rotated bone with bone-Z. The dot-product this second vector forms with its matrix-rotated version, will be the cosine of Twist.

One caveat to my suggestion, is that Pan will at first be undefined, if Bend == 0.